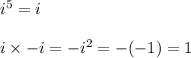Answer:
The multiplicative inverse of power of i are:
-
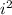 is '-1'
is '-1'
 is 'i'
is 'i'
-
 is '1'
is '1'
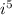 is '-i'
is '-i'
Explanation:
'i' is a complex number with the property such that:
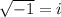
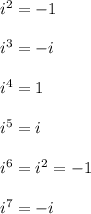
and so on.
" In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1"
The multiplicative inverse of :
since

-
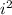 is '-1'
is '-1'
since
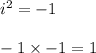
-
 is 'i'
is 'i'
since

-
 is '1'
is '1'
since
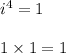
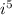 is '-i'
is '-i'
since