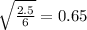Question

Find (a) the range and (b) the standard deviation of the data set 0.5,2.0,2.5,1.5,1.0,1.5 . Round to the nearest hundredth if necessary.

Answer 1

3

Explanation:

Answer 2

a.2

b.0.65

Explanation:

Given data

0.5,2.0,2.5,1.5,1.0,1.5

Highest value=2.5

Lowest value of data=0.5

Range=Highest value-Lowest value=2.5-0.5=2

Sum of given data=0.5+2+2.5+1.5+1+1.5=9

Total number of observations=n=6

Mean=
`\bar{x}=(sum\;of\;observation)/(number\;of\;observation)`

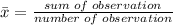
Using the formula

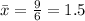
`\bar{x}=(9)/(6)=1.5`

x
`(x-\bar x)^2`

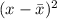
0.5 1

2.0 0.25

2.5 1

1.5 0

1.0 0.25

1.5 0

`\sum(x-\bar x)^2=1+0.25+1+0+0.25+0=2.5`

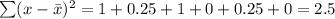
Standard deviation=
`\sqrt{(\sum(x-\bar x)^2)/(n-1)}`

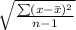
S.D=
`\sqrt{(2.5)/(6)}=0.65`