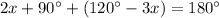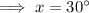Label the vertices of the quadrilateral A, B, C, D. Angle C is supplementary to the angle of measure 60 degrees, so its own measure is 120 degrees.
AD and BC are parallel, as are AB and CD, so ABCD is a parallelogram. This means angle A also has measure 120 degrees. The angle adjacent to the one with measure
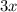 , part of angle A, then has measure
, part of angle A, then has measure
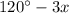 .
.
The three angles above the line through vertex A are supplementary, so we have