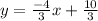Question

A circle with center C (4,-2) contains the point D (8,1). What is the equation of the line perpendicular to the radius of the circle passing through point C?

Answer 1

Explanation:

Answer 2

`y=(-4)/(3)x+(10)/(3)`

Explanation:

A circle with center C (4,-2) contains the point D (8,1).

Lets find out the slope of the line that contains point C and D

Slope =
`(y_2-y_1)/(x_2-x_1)`

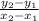
C (4,-2) is (x1,y1) and D (8,1) is (X2,y2)

Slope =
`(1+2)/(8-4)=(3)/(4)`

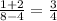
To get slope of perpendicular line we take negative reciprocal of 3/4 that is -4/3

the line passes throught point C

m= -4/3 , point (4,-2)

Use point slope formula

y-y1=m(x-x1) x1= 4, y1= -2, plug in all the values

`y+2=(-4)/(3)(x-4)`

`y+2=(-4)/(3)x+(16)/(3)`

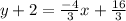
Subtract 2 on both sides

`y=(-4)/(3)x+(10)/(3)`