Answer:
(1,-1) is a valid solution for the inequality.
Explanation:
Given the graph of function we have to find the solution for inequality
Lets take the two points passing through the graph let it be (1,2) and (2,5).
Equation of line passing through the above two points are
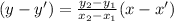
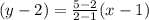
⇒
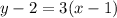
⇒
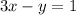
To find the inequality equation, put any point which comes in shaded region to above equation and put the sign of that inequality which gives the true condition. (3x-y=3(1)-0=3>1)
Hence, the inequality becomes 3x-y>1
To find the valid solution put the points one by one in above inequality and get the result.
(0,0) : 3(0)-0=0>1, False
(2,5) : 3(2)-5=1>1, False
(1,-1) : 3(1)-(-1)=4>1, True
(-1,-4) : 3(-1)-(-4)=1>1, False
Hence, (1,-1) is a valid solution for the inequality