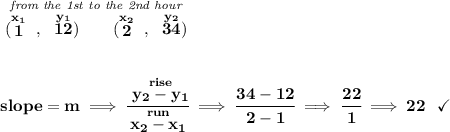Question

During with interval was the bicyclists speed the greatest?

Answer 1

check the picture below.

namely, which of those intervals has the steepest slope, recall slope = average rate of change.

now, from the picture, notice, those two there are the steepest, the other three are leaning too much to the "ground".

so, from those two, which is the steepest anyway? let's check their slope.

`\bf \stackrel{\textit{from the 6th to the 8th hour}}{(\stackrel{x_1}{6}~,~\stackrel{y_1}{104})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{146})} \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{146-104}{8-2}\implies \cfrac{42}{2}\implies 21~~\bigotimes \\\\[-0.35em] \rule{34em}{0.25pt}`

`\bf \stackrel{\textit{from the 1st to the 2nd hour}}{(\stackrel{x_1}{1}~,~\stackrel{y_1}{12})\qquad (\stackrel{x_2}{2}~,~\stackrel{y_2}{34})} \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{34-12}{2-1}\implies \cfrac{22}{1}\implies 22~~\checkmark`