Question

What is thr exact perimeter and are of the figure in the coordinate plane?

Answer 1

• perimeter ΔABC=
  `8√(5)+4√(2)units`

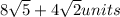
• area ΔABC=64-(16+16+8)=24 square units.

Explanation:

• The perimeter of triangle is the length of all the sides of a triangle.

in order to calculate the lengths of side AB,AC and BC we need to use the pythagorean theorem for triangles ADB,AEC and BFC.

for ΔADB:

`(AB)^(2)=(AD)^(2)+(DB)^2\\\\(AB)^(2)=4^2+8^2=16+64=80\\\\AB=4√(5)`

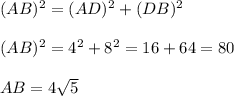
similarly for ΔAEC

`(AC)^(2)=(AE)^(2)+(EC)^2\\\\(AC)^(2)=4^2+4^2=16+16=32\\\\AB=4√(2)`

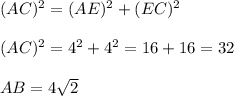
similarly for ΔBFC

`(BC)^(2)=(BF)^(2)+(FC)^2\\\\(BC)^(2)=8^2+4^2=16+64=80\\\\AB=4√(5)`

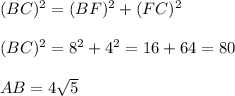
Hence, perimeter of ΔABC= AB+AC+BC=
`4√(5)+4√(2)+4√(5)`

=
`8√(5)+4√(2)units`

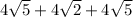
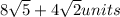
• Now area of ΔABC=area of square DBFE-( area ΔADB+ area ΔAEC+ area ΔBFC)

area of square DBFE= (side)^2

since the length of the side of square DBFE=8 units.

Hence, Area of square DBFE= (8)^2=64 square units.

Area of triangle is given as:
`(1)/(2)bh`

where b denotes the base of the triangle and h denotes the height of triangle and for right angled triangle it is equal to the perpendicular side.

for ΔADB; h=4 units and b=8 units

Hence, area ΔADB=
`(1)/(2)* 4* 8=16 square units`

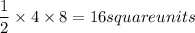
for ΔAEC ; h=4 units ,b=4 units

Hence, area ΔAEC =
`(1)/(2)*4*4=8 squareunits`

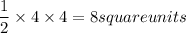
for ΔBFC ; h=8 units and b=4 units

Hence area of ΔBFC=
`(1)/(2)* 4* 8=16 square units`

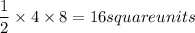
Hence area ΔABC=64-(16+16+8)=24 square units.