Question

Consider rational expressions in which the degree of the numerator is greater than that of the denominator and rational expressions in which the degree of the numerator is equal to that of the denominator. write a rule for the degree of the simplified expression for those two cases. do not worry about remainders.

please help this is so confusing. thank you much appreciated.

Answer 1

Rule: The degree of the simplified expression will be the difference of the degrees of numerator and denominator.

Step-by-step explanation:

Exponent Rules

In order to write the rule this question asks for, it is helpful to know the rules of exponents as they relate to division.

You may recall that ...

`(x\cdot x\cdot x)/(x\cdot x)=x \quad\text{factor cancellation}\\\\=(x^3)/(x^2)=x^(3-2)=x^1=x \quad\text{using exponents}`

In short, ...

`(x^a)/(x^b)=x^(a-b)`

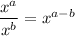
Degree of Rational Expressions

For the most part, there are only two things we are usually asked to care about with respect to rational expressions:

1. the zeros of the denominator (asymptotes or holes in the function graph)
2. the relative degree of numerator and denominator (end-behavior)

For the purpose of the second of these—seemingly the focus of this question—we are only concerned with the degree of the highest-degree term in each of the numerator and denominator.

Example: (x^3 -5x^2 -2x +24)/(x^2 +x -6) has a degree-3 term in the numerator and a degree-2 term in the denominator.

The exponent rule above tells you that the degree of the simplified expression will be the difference of the degrees of numerator and denominator. (This is true for both of the cases you're asked to consider here.)

_____

Why this is Interesting

The simplified expression (ignoring remainders) tells you the end behavior of the rational function. That is, if the degree of the simplified expression is 0 (numerator and denominator have the same degree), the simplified expression is a constant. That constant is the horizontal asymptote of the rational expression.

If the degree of the simplified expression is 1 (as in our example above), then the simplified expression is a line, or "slant asymptote". The graph attached shows this slant asymptote (orange) along with the plot of the rational function (purple).

The difference in degrees can be more than 1, in which case the end behavior (for large values of "x") will be that of the higher-degree function. For example, when the numerator degree is 2 more than the denominator degree, the asymptotic behavior of the rational function will be a parabola.