Answer:

Explanation:
Polynomial is a name made of two terms: poly and nomial where poly means many and nomial means terms. Thus, polynomial can be defined as an expression that is a sum of many terms expressed different powers of same variable.
For example:
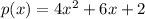 is an example of a polynomial.
is an example of a polynomial.
To find roots of a polynomial, we equate p(x ) to 0 i.e.
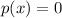 .
.
Whenever the roots are in radical form, it implies that they will occur as conjugates.
Conjugates means that if one of the root of an equation is
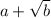 , the other root will be
, the other root will be
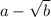 . To show that this is true and that the second root is of form
. To show that this is true and that the second root is of form
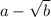 , we create a polynomial from the factors.
, we create a polynomial from the factors.
Factors are as follows:
 and
and
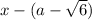
Polynomial
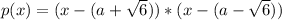
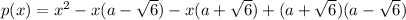
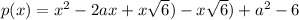
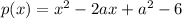
which is an quadratic equation.
Now if we try to solve this equation by using the quadratic formula we get:
![x = 1/2 [ 2a + \sqrt{4 a^(2)- 4( a^(2)- 6)}]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9xh4imissjblwfikw7iik2av8s41xk4nhx.png) and
and
![1/2 [ 2a - \sqrt{4 a^(2)- 4( a^(2)- 6)}]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sq4dt9us203fxfrwdy24snq7150t812uz0.png)
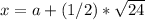 and
and
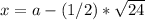
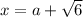 and
and
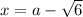
Thus we get square roots of form
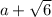 and
and
 .
.