Answer:
324 cubes.
Explanation:
Let n be the number of cubes with edge length 1/12 meter.
We have been given the lengths of edges of a right rectangular prism as
 meter,
meter,
 meter and
meter and
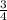 meter.
meter.
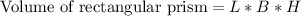 , where,
, where,
L = Length of prism,
B = Breadth of prism,
H = Height of prism.
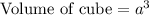 , where a= length of each edge of the cube.
, where a= length of each edge of the cube.
The volume of n cubes with each edge 1/12 will be equal to the volume of rectangular prism.
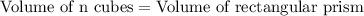
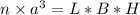
Upon substituting our given values we will get,
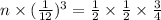

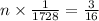
Let us multiply both sides of our equation by 1728.


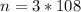
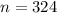
Therefore, 324 unit cubes can fit inside the given right rectangular prism.