Question

Physics question!
i did this wrong and don’t know how to fix it please help!

Answer 1

We're talking about an object starting at 127.8 m/s and ending at a complete stop. So in the 'Sub' line, v(final) should be zero.

Everything else looks good, so that one little change should get you there.

Answer 2

The issue with your answer is that you didn't choose the correct values for
`v_f` and
`v_0`.

We are only concerned with the movement of the jet on the ground between the moment it lands and the moment it completely stops (check the hint). This means its speed goes from its landing speed to zero.

Let
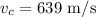`v_c = 639 \textrm{ m/s}` denote the cruising speed. Then we now the initial speed (i. e., the landing speed) is 20% of the cruising speed:

`v_0 = 0.2v_c = 0.2 * 639 \textrm{ m/s} = 127.8\textrm{ m/s}.`

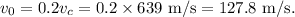
On the other hand, the final speed is simply zero, since jet comes to a complete stop:

`v_f = 0\textrm{ m/s}.`

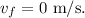
We now apply Torricelli's equation:

`v_f^2 = v_0^2 + 2ax,`

where
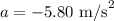`a=-5.80\textrm{ m/s}^2` is the acceleration and
`x` is the distance travelled. Solving for
`x`, we get:

`x= (v_f^2-v_0^2)/(2a).`

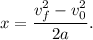
Substituting the numerical values, we get:

`x= (v_f^2-v_0^2)/(2a) = (0^2-127.8^2)/(2*(-5.80)) = (-16332.84)/(-11.60) \approx 1408.00\textrm{ m}.`

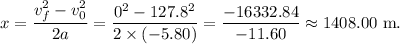
Which means the jet travels about
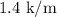`1.4\textrm{ k/m}` before coming to a complete stop, which is a much more reasonable value than
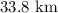`33.8\textrm{ km}`.