Question

The box plots below show student grades on the most recent exam compared to overall grades in the class:

Which of the following best describes the information about the medians?


The exam median is only 1–2 points higher than the class median.


The exam median is much higher than the class median.


The additional scores in the second quartile for the exam data make the median higher.


The narrower range for the exam data causes the median to be higher.

Answer 1

The statement that best describes the information about the medians is:

The additional scores in the second quartile for the exam data make the median higher.

Explanation:

• From the box plot we see that the class median is between 80-90 i.e. approx 85

and the exam median is approx 93.

Hence, the difference is more than 1-2 points.

Hence, option: A is incorrect.

• Also, there is not a big difference in the median

Since, the percent change in median is:

`=(93-85)/(85)* 100\\\\\\=9.4118\%`

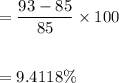
which is a small change.

Hence, option: B is incorrect.

• The additional scores in the second quartile for the exam data make the median higher.

As we know that the second quartile is the median of the data and adding additional score will obviously make the median higher.

• No, the narrower range for the exam data does not cause the median to be higher as the median is always located in the middle of the data .

Answer 2

The class median is around 85, the test median is around 95, so they are more than 1-2 points apart.

The median is the middle number of the data set, so this would not have anything to do with the number of scores used.

The answer should be: The exam median is much higher than the class median.