Question

What is the nth term rule of the quadratic sequence below?

6
,
20
,
40
,
66
,
98
,
136
,
.
.
.

Answer 1

3n² + 5n - 2

Explanation:

Given sequence:

6, 20, 40, 66, 98, 136, ...

Calculate the first differences between the terms:

`6 \underset{+14}{\longrightarrow} 20 \underset{+20}{\longrightarrow} 40 \underset{+26}{\longrightarrow} 66 \underset{+32}{\longrightarrow} 98 \underset{+38}{\longrightarrow} 136`

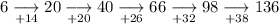
As the first differences are not the same, calculate the second differences:

`14 \underset{+6}{\longrightarrow} 20 \underset{+6}{\longrightarrow} 26 \underset{+6}{\longrightarrow} 32 \underset{+6}{\longrightarrow} 38`

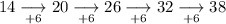
As the second differences are the same, the sequence is quadratic and will contain an n² term.

The coefficient of the n² term is half of the second difference.

Therefore, the n² term is: 3n²

Compare 3n² with the given sequence:

`\begin{array}\cline{1-5} n & 1 & 2 & 3 & 4\\\cline{1-5} 3n^2 & 3 & 12 & 27 & 48 \\\cline{1-5} \sf operation & +3&+8 & +13 & +18 \\\cline{1-5} \sf sequence & 6 & 20 & 40 & 66\\\cline{1-5}\end{array}`

The second operations are different, therefore calculate the differences between the second operations:

`3 \underset{+5}{\longrightarrow} 8 \underset{+5}{\longrightarrow} 13\underset{+5}{\longrightarrow} 18`

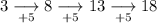
As the differences are the same, we need to add 5n as the second operation:

`\begin{array}c\cline{1-5} n & 1 & 2 & 3 & 4\\\cline{1-5} 3n^2 +5n & 8&22 & 42 & 68\\\cline{1-5}\sf operation & -2 &-2 &-2 & -2 \\\cline{1-5} \sf sequence & 6 & 20 & 40 & 66\\\cline{1-5}\end{array}`

Finally, we can clearly see that the operation to get from 3n² + 5n to the given sequence is to subtract 2.

Therefore, the nth term of the quadratic sequence is:

3n² + 5n - 2