Answer:
The correct option is 1.
Explanation:
In a graph, the lowest points of the functions are called local minima and highest points of the functions are called local maxima.
The point of local maxima and local minima can be more than one point. The graph must be continuous at extreme points.
From the given graph it is noticed that the highest point of the function is (0,1), therefore the local maxima is (0,1).
The lowest points of the graph are

But the graph is discontinuous at
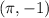 . So, the point
. So, the point
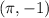 is not a local minima.
is not a local minima.
The point of local minima are
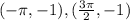 .
.
Therefore option 1 is correct.