Question

Casey can install a fountain in a school garden in 20 hours. Samuel can install a similar fountain in the same school garden in 30 hours. If they work together, they would take a total of t hours to install the fountain. Write an algebraic expression in terms of t for the fraction of the fountain they can install together in one hour. Write an equation for t. Solve for t to find the total number of hours they would take to install the fountain if they work together.

Answer 1

Answer: The answer is 1.2 hours.

Step-by-step explanation: Given that Casey and Samuel can install a fountain separately in 20 hours and 3 hours respectively. Working together, they take 't' hours to install the fountain.

In 1 hours the part of the fountain that Casey install =
`(1)/(20).`

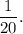
In 1 hour, the part of the fountain that Samuel install =
`(1)/(30).`

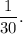
Together, in 1 hour, they will install
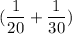`((1)/(20)+(1)/(30))` part of the fountain.

Also, it is given that they take 't' hours together to install the fountain, so in 1 hour, they will install
`(1)/(t)` part of the fountain.

Therefore, we can write

`(1)/(t)=(1)/(20)+(1)/(30),` which is the expression for 't'.

Solving this equation, we get

`(1)/(t)=(30+20)/(60)\\\\\Rightarrow(1)/(t)=(50)/(60)\\\\\Rightarrow t=(6)/(5)=1.2.`

Thus, they both complete installing the fountain in 1.2 hours while working together.

Answer 2

Answer: The required equation is
`(1)/(t)=(1)/(20)+(1)/(30)`.

They will take 1.2 hour to install the fountain in school if they wirk together.

Explanation:

Given: The time taken by Casey to install a fountain in a school= 20 hours

The time taken by Samuel to install the same fountain in school= 30 hours

Let t be the time of installation of fountain if they work together, then we have the following equation:-

`(1)/(t)=(1)/(20)+(1)/(30)\\\\\Rightarrow(1)/(t)=(30+20)/(20*30)\\\\\Rightarrow\ (1)/(t)=(50)/(60)\\\\\Rightarrow\ t=(60)/(50)\\\\\Rightarrow\ t=1.2`

Hence, they will take 1.2 hour to install the fountain in school if they wirk together.