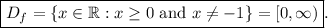Question

Do anyone know how to solve this problem

Answer 1

The domain is
`\boxed{D_f = [0, \infty)}`.

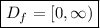Explanation:

Let
`f(x) = (√(2x))/(x+1)`.

Since we have a fraction, we need to make sure that its denominator isn't zero, since division by zero isn't defined. This means that:

`x+1 \\eq 0 \iff x \\eq -1.`

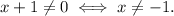
On the other hand, there's also a square root, whose argument can't be negative. This means that:

`2x \geq 0 \iff x \geq 0.`

So the domain is:

`\boxed{D_f =\{x\in\mathbb{R}: x\geq 0 \textrm{ and } x \\eq -1\} = [0, \infty)}.`