Question

Factor by Grouping.

The ac product of 35x² + 41x + 12 is
The factors of the ac product that add to 41 are
35x² + 41x + 12 =
Submit Question

Answer 1

y=35x²+41x+12

Here

• a=35 and c=12

So

• AC=35(12)=420

Now

Factors that add up to 41 are 21 and 20

Now solve

• 35x²+41x+12=0
• 35x²+21x+20x+12
• 7x(5x+3)+4(5x+3)
• (7x+4)(5x+3)

Answer 2

AC Factor: 420

Factors that add up to 41: 20 and 21

Rewritten equation:
`(35x^2+21x)+(20x+12)`

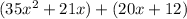
Explanation:

so a quadratic equation is generally expressed as
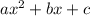`ax^2+bx+c`. So in this polynomial 35=a and c=12. The ac product would thus be (35)(12) which is 420

The factors of the AC product include: 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20 , 21, 28, 30, 35, 42, 60, 70, 84, 105, 140, 210 and 420. Since we're looking for a bigger number which is 41 you would generally want to look near the middle. and you can disregard any factors equal to or above 42. since they wouldn't add to 41. So I'll start at 30. 420/30 = 14 and 30 + 14 = 44 which is pretty close. Alright I'll try 28 instead. 420/28 = 15 and 15+28 = 43 which is also pretty close so I'll try the next factor 420/21 = 20 and 20+21 = 41! so the two factors are 20 and 21

Now using these two factors you can rewrite the equation as

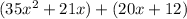`(35x^2+21x)+(20x+12)` which simplifies to the same quadratic equation