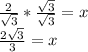Question

Simplify: 2(6+1)-|-10|=3x2

Answer 1

`(2\sqrt3)/(3) = x`

Explanation:

So you want to use PEMDAS to do the equation in order. This means that you'll start by adding 6 and 1 and then multiplying that value by 2

`2(7)-|-10| = 3x^2`

`14-|-10|=3x^2`

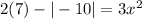
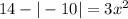
The absolute value can be defined as the "distance" from 0 which is going to be positive. You can think of it as the positive value of a number so if you have |-b| it will become b, and even if it's already positive, it will remain positive. so the absolute value of -10 is 10 but then it becomes negative again because of the subtraction

`14-10=3x^2`

`4=3x^2`

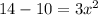
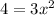
Now you want to solve for x by dividing both sides by 3 and taking the square root of both sides to isolate x

`(4)/(3) = x^2`

`\sqrt{(4)/(3)}=x`

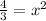
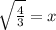
You can distribute the square root across division since
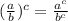`((a)/(b))^c = (a^c)/(b^c)` and the square root can be defined as
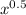`x^(0.5)` since
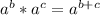`a^b * a^c = a^(b+c)` because if you spread it out it's really just
`(a * a * a ... b\ amount \ of \ times) * (a * a * a ... c\ amount\ of\ times)` which can be simplified to (a * a * a... (b + c) amount of times) if that makes any sense. Anyways using this property you'll get
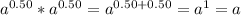`a^(0.50) * a^(0.50) = a^(0.50 + 0.50) = a^1 = a`. If you look at it you'll notice a^0.50 multiplied by it self gives you a... sounds like the square root, which it is. So now the equation becomes

`(√(4))/(√(3))=x`

`(2)/(\sqrt3)`

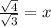
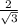
Now if you look at the equation you'll notice there's a radical in the denominator, which can be rationalized by multiplying by sqrt(3)\sqrt(3) which is 1 except it makes the denominator 3 and keeps the original value

`(2)/(\sqrt3) * (\sqrt3)/(\sqrt3)=x\\(2√(3))/(3) = x`