Question

Find the lengths of the missing sides in the triangle. Write your answers as integers or as decimals rounded to the nearest tenth.​

Answer 1

The last one
`(x=11.3, y=8)`.

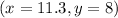Explanation:

1) There are three trigonometric ratios for right-angled triangles.

`sin()=(opposite)/(hypotenuse)\\cos()=(adjacent)/(hypotenuse)\\tan()=(opposite)/(adjacent)`

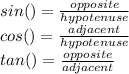
In a right triangle, the hypotenuse, h, is the side opposite the right angle. Relative to the acute angle θ, check the attachment, the legs are called the opposite side, o, and the adjacent side a.

2) In this case, we are given a length and an angle to find x and y.

Let's find x first. To find x we need to use
`sin()=(opposite)/(hypotenuse)`.

`sin(45)=(8)/(x)\\sin(45)x=8\\x=(8)/(sin(45)) \\x=11.31`

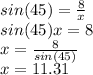
Find y.

Notice that, we can use the Pythagorean Theorem
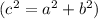`(c^2=a^2+b^2)` to find y.

`c^2=a^2+b^2`

`11.31^2=8^2+b^2\\11.31^2 - 8^2 = b^2\\63.9161 = b^2\\√(63.9161) = b\\b = 7.99`

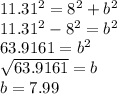
3) Round them off to the nearest tenth.

`x=11.31\\x=11.3`

`y=7.99\\y=8`

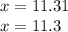
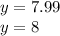
Therefore, the correct choice is the last one
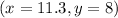`(x=11.3, y=8)`.