the given point p is located on the unit circle State the quadrant and find the angle also sin,cos,tan - QAmmunity.org

the given point p is located on the unit circle State the quadrant and find the angle also sin,cos,tan

asked Feb 19, 2020 212k views

2 Answers

Answer with explanation:

We know that any point located at (x,y)

Also, if the x-value and y-value both are positive then the point lie in first quadrant.

if both are negative then it lie in third quadrant.

If x-value is positive and y-value is negative then it lie in the fourth quadrant.

If x-value is negative and y-value is positive then it lie in the second quadrant.

The
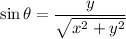
$\sin \theta=(y)/(√(x^2+y^2))$

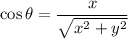
$\cos \theta=(x)/(√(x^2+y^2))$

and
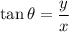
$\tan \theta=(y)/(x)$

1)

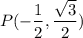
P(-(1)/(2),(√(3))/(2))

as x-value is negative and y-value is positive.

Hence, the point lie in the second quadrant.

Also,

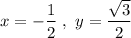
$x=-(1)/(2)\ ,\ y=(√(3))/(2)$

Hence,

$√(x^2+y^2)=\sqrt{((-1)/(2))^2+((√(3))/(2))^2}\\\\\\√(x^2+y^2)=\sqrt{(1)/(4)+(3)/(4)}\\\\\\√(x^2+y^2)=1$

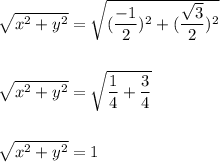
Hence, we have:

$\sin \theta=((√(3))/(2))/(1)\\\\\\\sin\theta=(√(3))/(2)$

$\cos \theta=(-1)/(2)$

and
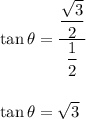
$\tan \theta=((√(3))/(2))/((1)/(2))\\\\\\\tan \theta=√(3)$

2)

P(0,-1)

As x-value is zero and y-value is negative.

Hence, the point lie on negative y-axis.

Also,

$x=0\ ,\ y=-1$

Hence,

$√(x^2+y^2)=√((0)^2+(-1)^2)\\\\\\√(x^2+y^2)=1$

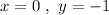
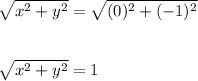
Hence, we have:

$\sin \theta=(-1)/(1)\\\\\\\sin \theta=-1$

$\cos \theta=(0)/(1)=0$

and
$\tan \theta=(-1)/(0)$ ,

Hence, we have: tan θ= undefined

3)

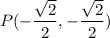
P(-(√(2))/(2),-(√(2))/(2))

which is same as:

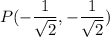
P(-(1)/(√(2)),-(1)/(√(2)))

As both the points are negative, hence the point lie in the third quadrant.

Also,

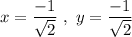
$x=(-1)/(√(2))\ ,\ y=(-1)/(√(2))$

Hence, we have:

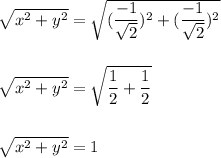
$√(x^2+y^2)=\sqrt{((-1)/(√(2)))^2+((-1)/(√(2)))^2}\\\\\\√(x^2+y^2)=\sqrt{(1)/(2)+(1)/(2)}\\\\\\√(x^2+y^2)=1$

Hence, we have:

$\sin \theta=(-1)/(√(2))$

$\cos \theta=(-1)/(√(2))$

$\tan \theta=1$

Tobs answered Feb 25, 2020

by Tobs

4.8k points

Search QAmmunity.org