Question

For a person standing 100m from the center of the base of the excel tower, the angle of elevation to the top of the tower is 71.6 degrees. How tall is the effect tower

Answer 1

To determine the height of the tower, we will use trigonometry, specifically the tangent function. Here's a step-by-step solution:

1. **Understanding the Problem:**
We have a right triangle where:
- The distance from the person to the base of the tower is the adjacent side of the triangle (100 meters).
- The height of the tower is the opposite side of the triangle, which we need to find.
- The angle of elevation from the ground to the top of the tower is 71.6 degrees.

2. **Using the Tangent Function:**
The tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. In mathematical terms for our case:
\[\tan(\theta) = \frac{\text{Height of tower}}{\text{Distance from base}}\]
Here, \(\theta\) is the angle of elevation (71.6 degrees).

3. **Solving for the Height of the Tower:**
Rearrange the equation to solve for the height of the tower:
\[\text{Height of tower} = \tan(\theta) \times \text{Distance from base}\]

4. **Calculating the Tangent of the Angle:**
First, convert the angle from degrees to radians since the tangent function in most calculators and mathematical equations uses radians. However, to maintain a straightforward teaching approach, we might not delve into the specifics of this conversion and instead simply use a scientific calculator, which can directly provide the tangent of an angle in degrees.

Now, calculate the tangent of 71.6 degrees.

5. **Finding the Height of the Tower:**
Input the values and calculate the height:
\[\text{Height of tower} = \tan(71.6^{\circ}) \times 100\]
Use your calculator to find the tangent of 71.6 degrees. Let's say it equals \(tan(71.6^{\circ}) \approx 3.001\).

6. **Final Calculation:**
Multiply the tangent of the angle by the distance from the base to get the height:
\[\text{Height of tower} \approx 3.001 \times 100\]
\[\text{Height of tower} \approx 300.1 \text{ meters}\]

So, the height of the tower is approximately 300.1 meters.

Answer 2

Given the statement: For a person standing 100 m from the center of the base of the excel tower, the angle of elevation to the top of the tower is 71.6 degrees.

Let h be the height of the Eiffel tower.

Angle of elevation is,
`\theta =71.6^(\circ)`

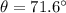
Distance of boy standing from the center of the base of the Eiffel tower is, 100 m.

Using tangent ratio:

`\tan \theta = \frac{\text{opposite side}}{\text{Adjacent side}}`

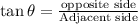
From the given figure as shown;

Solve for h;

`\tan 71.6 = (h)/(100)`

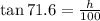
Multiply both sides by 100 we have;

`h = 100 \tan 71.6`

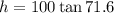
or

`h = 100 * 3.0061109035`

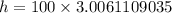
Simplify:

`h \approx 300 m`

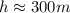
therefore, the height of the Eiffel tower is, 300m