I'm guessing you're given the function
 , and you're asked to find the inverse function
, and you're asked to find the inverse function
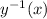 . To do this, swap
. To do this, swap
 and
and
 , then solve for
, then solve for
 :
:
![x=2-y^3\implies y^3=2-x\implies y=(2-x)^(1/3)=\sqrt[3]{2-x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kzg8z6mwb5mw3o8u16rakax46n5creodx0.png)
so that the inverse function is
![y^(-1)(x)=\sqrt[3]{2-x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jal8s6s2uo5r519lsu7csdwk10gqj6ysp2.png)
Just to verify:
![y(y^(-1)(x))=y(\sqrt[3]{2-x})=2-(\sqrt[3]{2-x})^3=2-(2-x)=x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rsbkyz8esq9us34dvxn63xlag6yjvucono.png)
![y^(-1)(y(x))=y^(-1)(2-x^3)=\sqrt[3]{2-(2-x^3)}=\sqrt[3]{x^3}=x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4xmf6xym86h5p5q3e5xbr1hlayowhzukk0.png)
But in case you're actually only interested in computing the square root, first we note that
 (the real-valued square root) is only defined as long as
(the real-valued square root) is only defined as long as
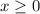 . So
. So
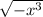 is defined as long as
is defined as long as
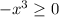 , or
, or
 , or equivalently
, or equivalently
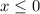 . Under this condition, we could write
. Under this condition, we could write

We can simplify this further, but we have to be careful. Suppose
 . Then
. Then
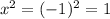 . But we get the same result if
. But we get the same result if
 , since
, since
 . There are two possible values of
. There are two possible values of
 that given the same value of
that given the same value of
 , so to capture both of them, we take
, so to capture both of them, we take
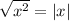 , the absolute value of
, the absolute value of
 . Then
. Then
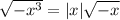
We can't simplify the square root term further than this.