Answer:
Will produce 'a slope with columns of parallel tangents'.
Explanation:
We have that the differential equation is a function of x only.
i.e.
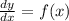 .
.
Let, F(x) be the anti-derivative if f(x) i.e.
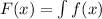
So, the differential equation gives,
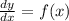 .
.
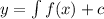
i.e. y = F(x) + c.
That means the general solution of the differential equation is a family of curves which are vertical copies of any one of them.
Hence, the differential equation that is a function of x only will produce 'a slope with columns of parallel tangents'.