Question

Calculate the time needed for a constant current of 0.961 a to deposit 0.500 g of co(ii) as

Answer 1

1.70 × 10³ seconds

Explanation

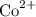`\text{Co}^(2+)` + 2 e⁻ →
`\text{Co}`

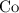
It takes two moles of electrons to reduce one mole of cobalt (II) ions and deposit one mole of cobalt.

Cobalt has an atomic mass of 58.933 g/mol. 0.500 grams of Co contains
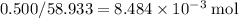`0.500 / 58.933 = 8.484* 10^(-3) \; \text{mol}` of Co atoms. It would take
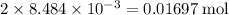`2 * 8.484 * 10^(-3) = 0.01697 \; \text{mol}` of electrons to reduce cobalt (II) ions and produce the
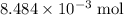`8.484* 10^(-3) \; \text{mol}` of cobalt atoms.

Refer to the Faraday's constant, each mole of electrons has a charge of around 96 485 columbs. The 0.01697 mol of electrons will have a charge of
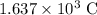`1.637 * 10^(3) \; \text{C}`. A current of 0.961 A delivers 0.961 C of charge in one single second. It will take
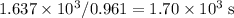`1.637 * 10^(3) / 0.961 = 1.70 * 10^(3) \; \text{s}` to transfer all these charge and deposit 0.500 g of Co.