Question

The median age for a first marriage in the United States for men was 28.1 in 2009 and 28.2 in 2010. Use an exponential model to predict the median age for men in 2019, where x is the number of years since 2009.

Answer 1

Explanation:

the ratio of growth can be calculated by median in 2010/median in 2009

28.2/28.1 = 282/281

in x years the median age = 28.1 * (282/281)^x

in 2019 (after 10 years) = 28.1 * (282/281)^10 = 29.1161671591

Answer 2

Answer: 29.2 in.

Explanation:

The general exponential function is given in the form:

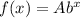`f(x)=Ab^x`, hwre A is the initial value , b is the growth factor and x is the time period.

Since, the growth factor is the ratio of the consecutive terms.

Therefore, the growth factor of the median age will be :

`b=(28.2)/(28.1)=1.003558\approx1.004`

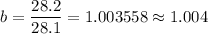
Take 28.1 as initial value , then the number of years from 2009 to 2019= 10 years

i.e. A = 28.1 , x=10 and b = 1.004

Then, the median age for men in 2019 will be :-

`f(10)=28.1(1.004)^(10)\\\\\Rightarrow\ f(10)=29.2444493259\approx29.2\ in.`

Hence, the the median age for men in 2019 = 29.2