Answer:
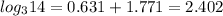
Step-by-step explanation:
Logarithms have the following property:
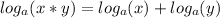
Taking into account the below property of logarithms, we can transform the initial problem in order to find a result. So we need to rewrite the exercise as:

Now we can use the property, replacing a by 3, x by 2, and y by 7, the we obtain:
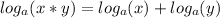

The values of
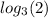 and
and
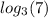 are known, so the last step is to replace that values:
are known, so the last step is to replace that values:
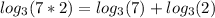
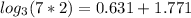
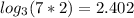
At the end the value of
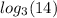 is 2.402
is 2.402