Answer: The correct graph is the graph (B).
Step-by-step explanation: We are given to select the graph that has figures which can undergo a similarity transformation to justify that they are similar.
We know that the two figures are similar if the ratio of the lengths of their corresponding sides are proportional.
In figure (A), the smaller figure is a square having side lengths of 1.5 units and 1.5 units.
The larger figure is a rectangle having length of 5 units and width of units.
So, the ratio of their corresponding sides are

Thus, the figures cannot be similar.
In figure (B), the smaller figure is a rectangle having length of 4 units and 2 units.
The larger figure is a rectangle having length of 6 units and width of 3 units.
So, the ratio of their corresponding sides are

Thus, the figures can be similar.
In figure (C), the smaller figure is a rectangle of lengths of 5 units and width 2 units.
The larger figure is a rectangle having length of 6 units and width of 3 units.
So, the ratio of their corresponding sides are
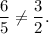
Thus, the figures cannot be similar.
In figure (D), the smaller figure is a rectangle of lengths of 3 units and width 2 units.
The larger figure is a rectangle having length of 6 units and width of 3 units.
So, the ratio of their corresponding sides are

Thus, the figures cannot be similar.
Thus, graph (B) is the correct option.