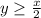Question

Your Student Government Association decided to do a fundraiser to raise money for a field trip. They decide to sell t-shirts and sweatshirts. The profit for each t-shirt is $10 and the profit for each sweatshirt is $15. They want to sell 50 items at most. Compared to t-shirts, they want to sellat least half as many sweatshirts, with a profit of at least $500.a. Write a system of inequalities that represents this situation.

NEED ANSWER ASAP

Answer 1

10x + 15y ≥ 500

x + y ≤ 50

`y\geq (x)/(2)`

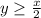
Explanation:

Let, the number of t-shirts = x and number of sweatshirts = y.

It is given that, at most 50 items are to be sold.

Thus, x + y ≤ 50.

Also, the number of sweatshirts to be sold is at least half the number of t-shirts.

Thus,
`y\geq (x)/(2)`

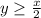
Further, it is given that the profit on t-shirts is $10 and on sweatshirts is $15 with the minimum total profit is $500.

So, we get 10x + 15y ≥ 500.

Hence, the system of inequality is given as:

10x + 15y ≥ 500

x + y ≤ 50

`y\geq (x)/(2)`