Question

What's the surface temperature of a woodstove with surface area 1.4 m2 that radiates energy at the rate of 18 kw? treat the stove as a blackbody?

Answer 1

Assuming the emissivity is 1.0, the temperature of the wood stove will be about 417 C

Step-by-step explanation:

You can use the Stefan-Boltzmann formula tying energy with temperature of a blackbody:

`P=\epsilon \sigma AT^4`

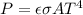
P - rate of radiation

`\epsilon` is the blackbody's emissivity

`\sigma = 5.67\cdot 10^(-8) (W)/(m^2\cdot K^4)` is the Stefan-Boltzmann constant

A - area

T - temperature

So,

`P=\epsilon \sigma AT^4\implies T = \sqrt[4]{(P)/(\epsilon \sigma A)}\\T = \sqrt[4]{(18000W)/(1.0\cdot 5.67\cdot 10^(-8) (W)/(m^2\cdot K^4)\cdot 1.4 m^2)}\approx 690K \approx 417^\circ C`

Assuming the emissivity ( a number between 0 and 1) is 1.0, the temperature of the wood stove will be about 417 C. The emissivity number was not given in your question. If you determine what it is, you can divide this result by the fourth power of that value to get an updated result.