Question

for the following data set calculate the percentage of data points that fall within one,two,and three standard deviation of mean. does the data appear to be normally distributed 20,12,19,40,22,25,10,24,36,23,15,22,23,13,18,19,17,32,24,21

Answer 1

The mean of the data set is 21.75

The standard deviation is 7.33

Percentage of data points that fall within one standard deviation is : 70%

Percentage of data points that fall within two standard deviation is : 95%

Percentage of data points that fall within three standard deviation is : 100%

Yes, the data appears to be normally distributed because half the data is more than the mean and half the data is less than the mean.

Explanation:

Let us Calculate the mean of the numbers first of all.

The formula for mean is :
`\frac {Sum\ of\ all\ data\ points}{Number\ of\ data\ points}`

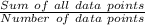
The mean, therefore, would be :
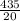`(435)/(20)` = 21.75

Now let's move towards calculating the standard deviation :

the formula for standard deviation is
`\sqrt{}(\sum (Data - mean)^(2))/(Number\ of\ data\ points)`

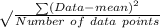
The calculation of standard deviation is shown in the attached file number 1 :

The standard deviation comes out to be 7.33.

Now, we to calculate which numbers fall within one standard deviation of the mean, we subtract the standard deviation from the mean to get the lower limit of the range and add standard deviation to the mean to get the upper limit of the range.

The first range of lower and upper limit will come out to be 14.416 to 29.084

We can just count the numbers in our data set that fall within this range.

Out of the 20 numbers 14 fall within this range and the percentage is 70%. (
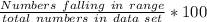`(Numbers\ falling\ in\ range)/(total\ numbers\ in\ data\ set) * 100` i.e.
`(14)/(20) * 100` )

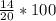Now, for calculating the numbers that fall within two standard deviations of the mean, we subtract the standard deviation twice from the mean to get the lower limit of the range and add standard deviation twice to the mean to get the upper limit of the range.

The second range comes out to be 7.08 to 36.41. We now count the numbers that fall within this range.

Out of the 20 numbers 19 fall within this range and the percentage is 95%. (
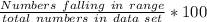`(Numbers\ falling\ in\ range)/(total\ numbers\ in\ data\ set) * 100` i.e.
`(19)/(20) * 100` )

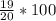Now, for calculating the numbers that fall within three standard deviations of the mean, we subtract the standard deviation thrice from the mean to get the lower limit of the range and add standard deviation thrice to the mean to get the upper limit of the range.

The third range comes out to be 0 to 43.75. We now count the numbers that fall within this range.

Out of the 20 numbers 20 fall within this range and the percentage is 100%. (
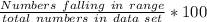`(Numbers\ falling\ in\ range)/(total\ numbers\ in\ data\ set) * 100` i.e.
`(20)/(20) * 100` )

The above range and calculation of data set is also shown in the attached picture number 2.

To calculate whether the data is normally distributed or not, we count how many numbers are more than the mean and how many are less than the mean. If 50% of the numbers (data points) in our data are less than the mean and 50% are more than the mean then, we will say that the data is normally distributed.

In this question the data is indeed normally distributed since, half the numbers are less than the mean and half of them are more than the mean. This is also shown is attachment number 3.