Answer:
D. No solution
Explanation:
We are given the system of equations as,
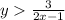 and
and
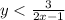 .
.
It is required to find the solution of the given system.
As we have that,
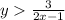
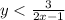 .
.
i.e. the values of y are strictly greater than
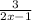 and strictly less than
and strictly less than
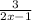 , no region will be a common part of the solution.
, no region will be a common part of the solution.
Also, it can be seen in the graph below that there does not exist any common solution of this system as there is dotted line that is dividing the regions.
Hence, no solution is the correct option.