Question

Find the diameter of a cone that had a volume of 56.52 cubic inches and a height of 6 inches

Answer 1

6 inches

Explanation:

The volume of a cone is 1/3
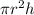`\pi r^2h`. We are given the volume and height, so substitute these values in and then solve for r. The radius is half of the diameter, so multiply the radius by two in the end to find the diameter.

1/3
`(1)/(3) \pi r^2(6)=56.52`

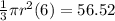
Multiply 1/3, pi, and 6 together.

`6.29r^2=56.52`

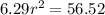
Divide both sides by 6.29.

`r^2=8.99`

Square root both sides.

r = 2.998

Multiply the radius 2.998 by 2 to find the diameter.

2.998 * 2 = 5.996

Since the volume was given in the hundredths place, we will round 5.996 to the hundredths: 6.

Answer 2

Answer: 5.98 inches

Explanation:

1. You have that the formula for calculate the volume of a cone is:

`V=(r^(2)h\pi)/(3)`

Where V is the volume, r is the radius and h is the height.

2. By definition, the diameter is twice the radius. Therefore, you need to solve for the radius:

`V=(r^(2)h\pi)/(3) \\3V=r^(2)h\pi\\r=\sqrt{(3V)/(h\pi)}`

3. Substitute values:

`r=\sqrt{(3(56.52in^(3)))/((6in)\pi)}=2.99in`

4. The diameter is:

`D=2r\\D=2(2.99in)\\D=5.98in`