Question

There a six bands competing in a competition. How many different ways can the 1st, 2nd, and 3rd place be awarded

Answer 1

There are 6 choices for 1st place, 5 choices for 2nd place, and 4 choices for 3rd place.

Each number (6,5,4) is one less than the previous one because once you choose the place for one of the bands, it can not receive another place.

Since each place is independent, you simply multiply 6,5, and 4 to get 120.

Answer 2

Answer: 120

Explanation:

Given : There a six bands competing in a competition.

To find : The number of different ways can the 1st, 2nd, and 3rd place be awarded.

We use permutations here since order matters.

Number of permutation of n things taking r at a time is given by :-

`^nP_r=(n!)/((n-r)!)`

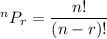
For n= 6 and r= 3 , we have the different ways can the 1st, 2nd, and 3rd place be awarded as:

`^6P_3=(6!)/((6-3)!)\\\\=(6*5*4*3!)/(3!)=120`

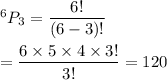
Hence, the 1st, 2nd, and 3rd place can be awarded in 120 ways.