Question

What are the vertices of the hyperbola with equation 4y^2 -25x^2=100

Answer 1

(0,-5) and (0,5).

Explanation:

We have been given that an equation of hyperbola
`4y^2-25x^2=100`.

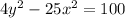First of all we will convert our given equation into the standard form of hyperbola.

Let us divide both sides of our equation by 100.

`(4y^2)/(100)-(25x^2)/(100)=(100)/(100)`

`(y^2)/(25)-(x^2)/(4)=1`

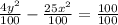
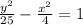
Since we know that the positive term in the equation of a hyperbola determines whether the hyperbola opens in the x-direction or in the y-direction. Our hyperbola has a positive
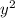`y^2` term, so it opens in the y-direction (up and down).

The equation of a vertical hyperbola is :
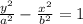`(y^2)/(a^2)-(x^2)/(b^2)=1`, where -a and a are vertices of our hyperbola.

`(y^2)/(5^2)-(x^2)/(2^2)=1`

`a^2=5^2`

`5^2=\pm5`

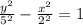
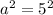
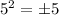
Upon comparing our equation with vertical hyperbola equation we can see that vertices of our hyperbola will be (0.-5) and (0,5).