Question

If a^2 and b are directly proportional, and a=2 when b=9, then what is b when a=6?

Answer 1

when ( a = 6 ), ( b = 81 ), indicating the direct proportionality between the squares of the values of ( a ) and ( b ).

Step-by-step explanation:

Direct proportionality between
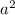`\( a^2 \)`and \( b \) means that when ( a ) increases by a certain factor, ( b ) will also increase by the square of that factor. Initially, \( a = 2 \) when ( b = 9 ). Therefore, the ratio of ( a ) to ( b ) is ( 2^2 : 9 = 4 : 9 ). To find ( b ) when ( a = 6 ), use this ratio.

Calculate the ratio between ( a ) and ( b ) at ( a = 6 ):

`\( 4 : 9 = 6^2 : x \)`

`\( 4 : 9 = 36 : x \)`

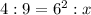
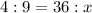
Cross multiply to find ( x ):

`\( 4x = 36 * 9 \)`

`\( 4x = 324 \)`

`\( x = (324)/(4) \)`

`\( x = 81 \)`

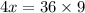
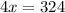
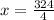
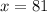
Therefore, when ( a = 6 ), ( b = 81 ), indicating the direct proportionality between the squares of the values of ( a ) and ( b ).

Answer 2

b = 81

Step-by-step explanation:

given a² and b are directly proportional then the equation relating them is

a² = kb ← k is the constant of proportionality

to find k use the condition a = 2 when b = 9 , then

2² = 9k

4 = 9k ( divide both sides by 9 )

`(4)/(9)` = k

a² =
`(4)/(9)` b ← equation of proportion

when a = 6 , then

6² =
`(4)/(9)` b

36 =
`(4)/(9)` b ( multiply both sides by 9 to clear the fraction )

324 = 4b ( divide both sides by 4 )

81 = b