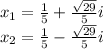Question

Solve each of the quadratic equations 0=5x^2-2x+6

Answer 1

Answer:
`x_1=(1)/(5)+(√(29))/(5)i\\x_2=(1)/(5)-(√(29))/(5)i`

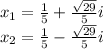
Explanation:

1. You can solve the quadratic equation by completing the square, as following:

- The leading coefficient must be 1, therefore, you need to divide the equation by 5:

`(5x^(2)-2x+6)/(5)=0\\x^(2)-(2)/(5)x+(6)/(5)=0`

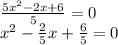
- Substract
`(6)/(5)` at both sides:

`x^(2)-(2)/(5)x+(6)/(5)-(6)/(5)=-(6)/(5)`

`x^(2)-(2)/(5)x=-(6)/(5)`

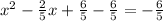
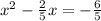
- Divide the coefficient of
`x` by 2 and and square it:

`((2)/((5)/(2)))^(2) =(1)/(25)`

- Add it to both sides:

`x^(2)-(2)/(5)x-(1)/(25)=-(6)/(5)+(1)/(25)`

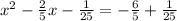
- Then:

`(x-(1)/(5))^(2) =-(29)/(25)`

`x-(1)/(5)=\sqrt{-(29)/(25)}`

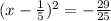
- Knowing that
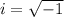`i=√(-1)`:

`x_1=(1)/(5)+(√(29))/(5)i\\x_2=(1)/(5)-(√(29))/(5)i`