Question

the city of Picayune has set aside $900,000 to build a new water tower in the shape of a cylinder. If the price per cubic foot is $10.50, what is the largest measure for the radius and height of the cylinder in order to not exceed the budget?

Answer 1

So as not to exceed the budget, where π = 22/7, we have;

The radius = 10 ft and the height = 3/11 ft

For standard 40 ft. height, the radius is approximately 0.8259 ft

Explanation:

The amount set aside for the water tower = $900,000

The price (amount) per cubic foot = $10.50

Therefore, we have;

`The \ volume \ of \ the \ water \ tower \ to \ be \ built = (The \ amount \ set aside \ for \ the \ water \ tower)/(The \ price \ (amount) \ per \ cubic \ foot )`

`\therefore The \ volume \ of \ the \ water \ tower \ to \ be \ built = (\$ 900,000)/(\$10.50/ft\\ ^3) = (600)/(7) ft.^3 = 85 (5)/(7) ft^3`

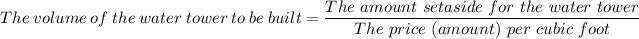
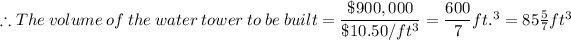
Whereby the height of a standard water tower = 40 ft., we have;

The shape of the water tower = The shape of the water tower

∴ The volume of the water tower V = π × r² × h

Where;

r = The radius of the water tower

h = The height of the water tower

Taking π = 22/7

600/7 = 22/7 × r² × h

r² × h = 600/7/(22/7) ≈ 300/11 = 100 × 3/11

Solving to get exact dimensions so as to not exceed the budget, we have;

r² × h = 100 × 3/11 = 10 × 10 × 3/11

Therefore, the radius can be 10 ft. and the height = 3/11 ft.

Or for standard 40 ft. height, we have;

r² = 600/7/(π × 40)

r ≈ 0.8259 ft.