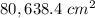Question

The circumference of the base of a right circular cylinder is 252 cm. Find the lateral surface area if the height is 3 m.​

Answer 1

The lateral surface area is
`80,638.4 \ cm^2`

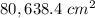
Explanation:

Lateral Surface Area of a Cylinder

It can be computed with the formula:

`\displaystyle A=\pi r^2+2\pi rh`

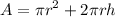
Where:

r = radius of the circular base

h = height

The circumference of the base can be calculated as:

`C = 2\pi r`

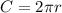
We are given the circumference C=252 cm, let's find the radius solving for r:

`\displaystyle r=(C)/(2\pi)`

`\displaystyle r=(252\ cm)/(2\pi)`

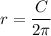
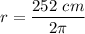
r = 40.1 cm

Now we calculate the lateral surface area knowing h=3 m=300 cm:

`\displaystyle A=\pi 40.1^2+2\pi 40.1*300`

`\boxed{A = 80,638.4 \ cm^2}`

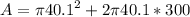
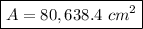
The lateral surface area is
`80,638.4 \ cm^2`