Answer:
The escape velocity on the planet is approximately 178.976 km/s
Step-by-step explanation:
The escape velocity for Earth is therefore given as follows
The formula for escape velocity,
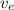 , for the planet is
, for the planet is
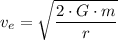
Where;
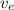 = The escape velocity on the planet
= The escape velocity on the planet
G = The universal gravitational constant = 6.67430 × 10⁻¹¹ N·m²/kg²
m = The mass of the planet = 12 × The mass of Earth,
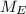
r = The radius of the planet = 3 × The radius of Earth,
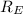
The escape velocity for Earth,
 , is therefore given as follows;
, is therefore given as follows;
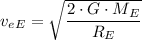
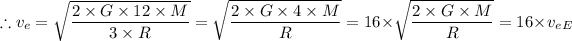
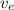 = 16 ×
= 16 ×

Given that the escape velocity for Earth,
 ≈ 11,186 m/s, we have;
≈ 11,186 m/s, we have;
The escape velocity on the planet =
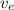 ≈ 16 × 11,186 ≈ 178976 m/s ≈ 178.976 km/s.
≈ 16 × 11,186 ≈ 178976 m/s ≈ 178.976 km/s.