Question

Please help me I really need to turn this in !!!! Please

Answer 1

Please check the explanation.

Explanation:

Part a)

Given the table

Year Value ($)

1 18,000

2 15,300

3 13,005

Let us check the sequence

18000, 15300, 13005,...

Let us find the common ratio 'r' of all the adjacent terms to check whether the sequence represents the geometric sequence or not, using the formula such as:

`\:r=(a_(n+1))/(a_n)`

`(15300)/(18000)=(17)/(20),\:\quad (13005)/(15300)=(17)/(20)`

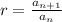
As the ratio of all the adjacent terms is the same, so

`r=(17)/(20)`

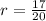
Therefore, the given sequence is a geometric sequence

Part b)

Given the sequence

18000, 15300, 13005,...

The nth term of the geometric sequence is

`a_n=a_1\cdot r^(n-1)`

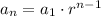
here

`a_1=18000`

`r=(17)/(20)`

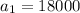
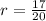
so

`a_n=18000\left((17)/(20)\right)^(n-1)`

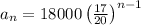
In order to determine the car worth in the 15th year, substitute n = 15

`a_(15)=18000\left((17)/(20)\right)^(15-1)`

`a_(15)=18000(17^(14))/(20^(14))`

`a_(15)=18000* \:\:0.10276`

`a_(15)=1850` $

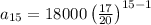
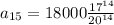
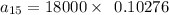
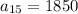Therefore, the worth of a car in the 15th year will be: $1850