Given:
Consider the completer question is "Find the derivative
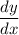 for
for
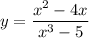 ."
."
To find:
The derivative
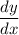 .
.
Solution:
Chain rule:
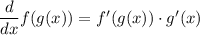
Quotient rule:
![(d)/(dx)(f(x))/(g(x))=(g(x)f'(x)-f(x)g'(x))/([g(x)]^2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/fbq8y3qm39duyrzqsb0i84pebjbkvx7u19.png)
We have,
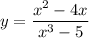
Differentiate with respect to x.
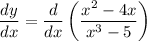
Using chain rule and quotient rule, we get
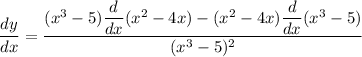
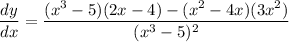
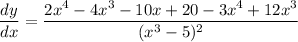
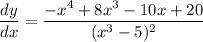
Therefore, the required answer is
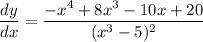 .
.