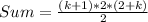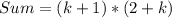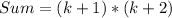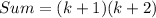Question

What is the sum of first k+1 even numbers

Answer 1

`Sum = (k+1)(k+2)`

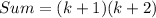
Explanation:

Given

k + 1 even numbers

Required

Their sum

This question will be solved using the sum of nth term of an AP

`S_n = (n)/(2)(2a + (n - 1)d)`

Where

a = the first even number

`a = 2`

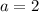
n = number of terms

`n =k +1`

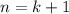
d = difference between consecutive even numbers

`d = 2`

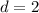
So, the expression becomes:

`Sum = (k+1)/(2)(2 * 2 + (k + 1 - 1) * 2)`

`Sum = (k+1)/(2)(2 * 2 + (k) * 2)`

`Sum = (k+1)/(2)(4 + 2k)`

`Sum = ((k+1)(4 + 2k))/(2)`

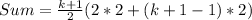
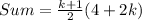
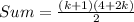
Factorize 4 + 2k

`Sum = ((k+1)*2*(2 + k))/(2)`

`Sum = (k+1)*(2 + k)`

`Sum = (k+1)*(k+2)`

`Sum = (k+1)(k+2)`