Answer:
See the answers below
Step-by-step explanation:
We can solve this problem using the principle of energy conservation. That is, the energy is conserved before and after dropping the bag.
For this case we have mechanical energy, which is the sum of the kinetic and potential energies.
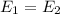
where:
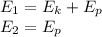
Ek = kinetic energy [J] (units of Joules)
Ep = potential energy [J]
In the final Energy (2), there is only potential energy. since when the balloon reaches the maximum height its velocity is zero, that is, there is no kinetic energy.
A)
![m*g*h+(1)/(2)*m*v^(2) =m*g*h_(1) \\9.81*50+0.5*(15)^(2)=9.81*h_(1)\\h_(1) = 61.46 [m]](https://img.qammunity.org/2021/formulas/physics/high-school/6gf1632aae7qdclu8khzgrd2ezvfz1uilo.png)
B)
With the value calculated above we can find the acceleration of the balloon.
The distance traveled is the difference between the maximum height and 50 meters.
![x = 61.46-50\\x = 11.46[m]](https://img.qammunity.org/2021/formulas/physics/high-school/i5y7ndfoyryz7sg0x58fj7vc3wqs7olf4p.png)
With the following equation of kinematics.
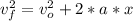
![0 = 15^(2) +2*a*11.46\\a = - 9.816 [m/s^(2) ]](https://img.qammunity.org/2021/formulas/physics/high-school/2bmlxaty80jsktwvat6k2abyk6ab77aoq0.png)
The negative sign indicates that the acceleration acts downward. That is, in the opposite direction to the movement.
We can use the following equation of kinematics to find the final velocity after 4 seconds.
![v_(f)=v_(o)-a*t\\v_(f)=15-9.816*(4)\\v_(f)=-24.24 [m/s]](https://img.qammunity.org/2021/formulas/physics/high-school/ykn2597e2xuh5ww5sd8whms9ns55e5om3v.png)
Now the distance:
![v_(f)^(2) =v_(o)^(2)-2*a*x\\(24.24)^(2) =(15)^(2) -2*9.81*x\\x = 18.48 [m]\\x_(f)=50+18.48 = 68.48 [m]](https://img.qammunity.org/2021/formulas/physics/high-school/hvz3rp8fmtktqx1q2uoafx3hhpg6yflyos.png)
c) Using the following equation of kinematics.
![v_(f)=v_(o)-a*t\\0 = 15-9.81*t\\15=9.81*t\\t = 1.52 [s]](https://img.qammunity.org/2021/formulas/physics/high-school/uik9odpk4lwpbsrv15wdn1p2pn9z08urwf.png)