Question

Find the exponential function of the 2 points (3, 7) and (5, 63). Use

the formula f(x) = a(b)”.

Answer 1

We obtained the two exponential functions:

• 
  `y\:=\:(7)/(27)\left(3\right)^x`

• 
  `y\:=-\:(7)/(27)\left(-3\right)^x`

Explanation:

As we know that the exponential function is of the form

f(x) = abˣ

Given the points

• (3, 7)

• (5, 63)

We know these points belong to the exponential function.

so substituting the values (3, 7) and (5, 63) in the function

putting (3, 7)

y = abˣ

7 = ab³

also putting (5, 63)

y = abˣ

63 = ab⁵

Considering the 2nd equation

63 = ab⁵

as

`a^b* \:a^c=a^(b+c)`

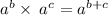
so

63 = ab³×b²

substituting 7 = ab³ in 63 = ab³×b²

63 = 7 × b²

b² = 63/7

b² = 9

b = ± 3

If b = 3

plug in b = 3 in the equation 7 = ab³ to find the value 'a'

7 = ab³

7 = a(3)³

7 = a × 27

a = 7/27

so, a = 7/27 and b = 3 would give us the function

y = abˣ

`y\:=\:(7)/(27)\left(3\right)^x`

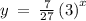
if b = -3

plug in b = -3 in the equation 7 = ab³ to find the value 'a'

`\:7\:=\:a\left(-3\right)^3`

`a\left(-27\right)=7`

`a=-(7)/(27)`

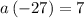
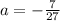
so, a = -7/27 and b = -3 would give us the function

y = abˣ

`y\:=-\:(7)/(27)\left(-3\right)^x`

Thus, we obtained the two exponential functions:

• 
  `y\:=\:(7)/(27)\left(3\right)^x`

• 
  `y\:=-\:(7)/(27)\left(-3\right)^x`