Question

At sea level, where g=9.80 m/s^2, a pendulum has a period of 1.000s. When you take it to the top of a mountain, its period is 0.9990s. What is g at the top of the mountain? (Keep 4 significant figures.) (Unit=m/s^2)

Answer 1

The g at the top of the mountain is 9.820 m/s².

Step-by-step explanation:

The period of simple pendulum is given as;

`T = 2\pi \sqrt{(l)/(g) }`

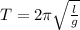
where;

T is period of the oscillation

g is acceleration due to gravity

l is length of the pendulum

`T = 2\pi \sqrt{(l)/(g) } \\\\(T)/(2\pi) = \sqrt{(l)/(g) }\\\\(T^2)/(4 \pi ^2) = (l)/(g)\\\\T^2 g = 4 \pi ^2 l\\\\let \ 4 \pi ^2 l = k\\\\T^2_(sea \ level) \ * \ g_(sea \ level) = T^2_(top \ of \ mountain) \ * \ g_(top \ of \ mountain)\\\\ g_(top \ of \ mountain) = (T^2_(sea \ level) \ * \ g_(sea \ level))/(T^2_(top \ of \ mountain) ) \\\\ g_(top \ of \ mountain) = (1^2 \ * \ 9.8)/(0.999^2) = 9.820 \ m/s^2`

Therefore, the g at the top of the mountain is 9.820 m/s².