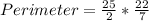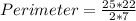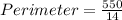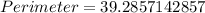Answer:
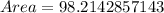
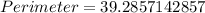
Explanation:
From the attachment, we have:
- 2 semicircles B and C
- 1 quarter circle CDE
- radius, r = 5cm
To calculate the total area of the figure, we have to calculate the areas of individual shapes, then add them together
For Semicircle B
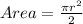
Substitute 5 for radius (r)

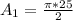
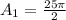
For Semicircle C
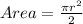
Substitute 5 for radius (r)
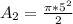
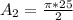
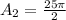
For Quarter circle DC
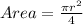
Substitute 5 for radius (r)
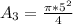
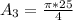
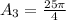
The area of the shape is:

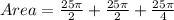
Take LCM
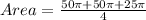
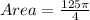
Take

So, we have:
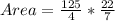
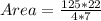
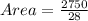
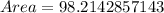
To calculate the total perimeter of the figure, we have to calculate the circumference of individual shapes, then add them together
For Semicircle B
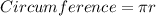
Substitute 5 for radius (r)
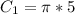
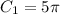
For Semicircle C
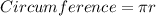
Substitute 5 for radius (r)
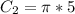
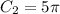
For Quarter circle DE
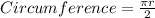
Substitute 5 for radius (r)
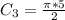
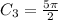
The perimeter of the shape is:
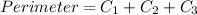
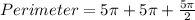
Take LCM
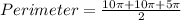
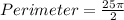
Take

So, we have: