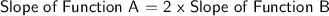Question

12. (03.03 MC) The equation below represents Function A and the graph represents Function B: Function A f(x) = 6x - 1 Function B 4 2 + 1 -2 1 -1 -2 -4 t -5​

Answer 1

Ans : = 0

Explanation:

Answer 2

`\textsf{Slope of Function A = 2 x Slope of Function B}`

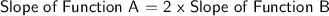
Explanation:

We know that Function A is given by:

`f(x)=6x-1`

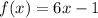
And we are given the graph of Function B.

And we are asked to compare the slopes of the two functions.

So, we will determine the slope of each.

For Function A, the slope is simply the coefficient of our independent variable x.

Since 6 is our coefficient, the slope of Function A is 6.

For Function B, we will utilize the slope formula, given by:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

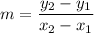
We will need any two points from our graph. Let’s use (0, 1) and (-1, -2).

So, we will let (0, 1) be (x₁, y₁) and (-1, -2) be (x₂, y₂). Substitute appropriately:

`\displaystyle m=(-2-1)/(-1-0)`

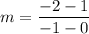
Evaluate:

`\displaystyle m=(-3)/(-1)=3`

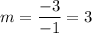
So, the slope of Function B is 3.

Therefore, the slope of Function A is twice the slope of function B.

So, we can write that:

`\textsf{Slope of Function A = 2 x Slope of Function B}`