Answer:
Co-efficient of
 is missing.
is missing.
It should be 8
 .
.
Explanation:
Given two polynomials:
1st polynomial:
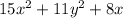
2nd polynomial:
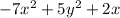
To find:
The value in the blank:
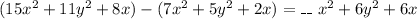
Solution:
Here, we have 3 pair of like terms.
2 terms with
 , 2 terms with
, 2 terms with
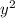 and 2 terms with
and 2 terms with
 .
.
Like terms can be subtracted.
Subtracting the terms with
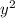 , the coefficients will get subtracted.
, the coefficients will get subtracted.
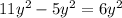
Subtracting the terms with
 , the coefficients will get subtracted.
, the coefficients will get subtracted.
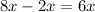
Subtracting the terms with
 , the coefficients will get subtracted.
, the coefficients will get subtracted.
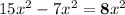
Therefore, the answer is:
Co-efficient of
 is missing.
is missing.
It should be 8
 .
.