Question

put the steps, for changing the formula for sector area of a circle in degrees to the formula for the sector area of a circle in radians, in the correct order​

Answer 1

see explanation

Explanation:

The area (A) of a sector is calculated as

A = area of circe × fraction of circle

= πr² ×
`(0)/(360)` ← where θ is in degrees

[ note that 360° = 2π radians ], then

A = πr² ×
`(0)/(2\pi )` ← where θ is in radians

( Cancel π on numerator/ denominator )

A =
`(1)/(2)`θr²

Answer 2

9514 1404 393

Answer:

top down: 2, 4, 1, 7, 6, 5, 3, 8

Explanation:

It appears the expected order may be ...

__

Write the formula for a sector area of a circle with central angle, θ, in degrees.

`\textit{Area of a Sector}=(\theta)/(360^(\circ))\cdot\pi r^2`

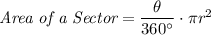
Replace 360° with 2π radians.

`(\theta)/(360^(\circ))=(\theta)/(2\pi)`

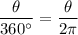
Replace the angle ratio in degrees with the angle ratio in radians.

`\textit{Area of a Sector}=(\theta)/(2\pi)\cdot\pi r^2`

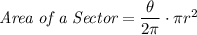
Simplify by cancelling

`\textit{Area of a Sector}=(1)/(2)\theta r^2`