Answer:
As the sample size increases, the variability decreases.
Explanation:
The actual departures from the mean are used to quantify variability. The variance would be lower the fewer the deviations.
By using the central limit theorem, we can determine that the sample mean for random samples of size n follows a normal distribution.
The standard deviation of the X bar will be
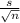 .
.
where s is the sample's variance's square root.
As a result, we discover that the standard deviation, or variability, is inversely proportional to the square root of the sample size. Therefore, standard error lowers as sample size grows. The variability falls off as sample size rises.